Concatenated Codes is a type of error-correcting code formed by the series combinations of two or even more codes to form a complex one. By this approach, a long length code is produced that increases the randomness thereby increasing the encryption ability. This facilitates more secured data communication.
Basically, the word ‘concatenation’ is used in reference to a serially interconnected orientation of something. Here in reference to coding, concatenation is the series combination of two different codes that forms a long stream of codes.
Content: Concatenated Code
History
Concatenated codes came into existence in the year 1965 and were introduced by David Forney an American Electrical Engineer, in relevance to a theoretical explanation. However, with technological advancements, the concept was improvised and became popular. Moreover, in the 1970s NASA started utilizing the concatenated codes as its standard tool for coding in space communication.
As we have discussed that concatenated codes are series interconnection, likewise there is another coding that includes parallel interconnection and it is known as turbo code. However, concatenated code was the first one that gained huge importance in space communication. Thus, turbo code and various other modern capacity similar coding techniques are considered as an elaboration of it.
Introduction to Concatenation Coding
We know that channel coding enables us to transmit a stream of data with redundancies over a communication channel at a high rate. Further, it is decoded at the other end so that original data can be obtained by the receiver even if errors are added during transmission.
For the process of encoding and decoding various algorithms are used that converts the actual bitstream into a coded data and then at the time of reception actual data is retrieved from the obtained coded stream.
Concatenated code is one such algorithm, used for the purpose of error correction of the bitstream. Basically, a concatenated code involves a cascade combination of a bitstream divided by applying separate error-correcting codes. More simply, a two-level coding is utilized here, that includes an inner code (binary in nature) and an outer code (non-binary in nature) which are two separate codes that serially transmitted over a channel.
This coding provides such a robust code that can correct burst errors generated by fading channels.
An interleaver plays a crucial role in concatenated coding approach as it helps in the random distribution of bursts of errors. To know more about how interleaving takes place, refer to the content interleaving.
It is to be noted here that generally RS code and convolutional code are concatenated together which gives rise to RS-CC concatenation. This is used as a standard for telemetry channel coding by space organizations.
Block Diagram for Concatenated Coding System
The figure shown below represents a basic concatenated coding system that was proposed in response to the theoretical explanation:
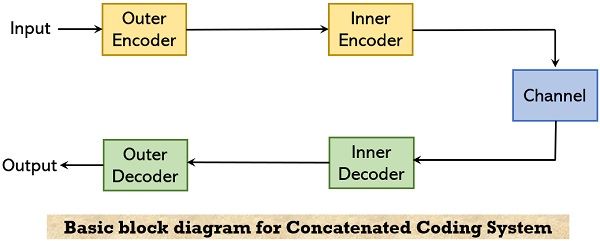
In the figure shown above, the coder-channel-decoder combination is regarded as a super-channel. Also, we design it in a way so that the output achieved corresponds to the correct input.
Here, the inner code considered was a short block code, of rate, block length, and codeword as r, n, and 2rn respectively. For decoding, an inner decoder is used that leads to an exponential rise in complexity with an increase in block length. The outer code taken here is an RS code i.e., Reed-Solomon code of length 2rn, and each element of it corresponds to an inner codeword.
Hence, in this case, the concatenated code generated will have an overall block length N as n2rn.
Basically, we can say, that by concatenating, long codes are achieved then are decoded by 2 decoders that are designed for decoding comparatively shorter codes. Due to this reason, it is said that this approach reduces complexity, by making compromises with performance.
Thus, in the 1970s, an improvised version came into existence that gained high popularity in space-related applications.
The figure shown below represents an improvised concatenated coding system:
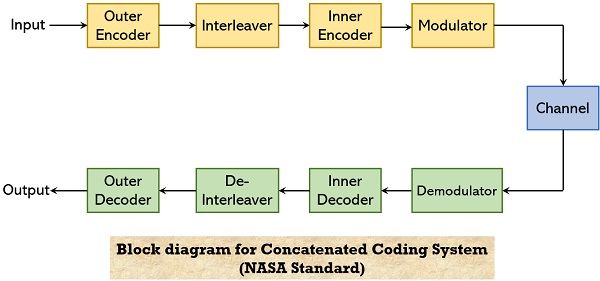
Here from the above figure, it can be concluded that the two improvisations are:
- Rather than using a block code as inner code, a convolutional code was used of short constraint length (having 64 states), for decoding of which Viterbi algorithm has been used. The reason behind using convolutional code rather than block code is that the convolutional code is less complex.
- Also, in the new model, interleaving and deinterleaving units were added. This was done to spread the bursty errors generated by the Viterbi decoder.
In the improvised model, the outer code remains as it was in the previous model i.e., non-binary BCH code known as Reed-Solomon code. The reason for this is these are the only general non-binary code known and its coding and decoding are comparatively easy.
Here, the operation takes place in a way that, the input code is fed to the outer encoder that performs encoding of RS code. Further, the interleaver unit comes into action and randomizes the bursty error segment from the encoded RS code. Once this is done, then the output of the interleaver reaches the inner encoder, within which encoding of convolutional code takes place.
A modulator unit present in this configuration modulates the received encoded bitstream which is further transmitted to the other end via a proper channel.
At the receiver end, a demodulator is present that performs demodulation of the received stream through the channel. The demodulated code is provided to the inner decoder that performs decoding of the convolutional code via the Viterbi algorithm. The output of the inner decoder is fed to the de-interleaver that performs the reverse operation of interleaver and produces a code with a burst of errors.
The bursty error code is provided to the outer decoder where decoding of RS code algebraically takes place. Thus, a long bitstream can be decoded in two parts thereby reducing the complexity associated with encoding and decoding such bitstream.
Conclusion
Thus, we can say that concatenated code helps in forming long codes from shorter ones. By this decoding, complexity can be reduced to large extents as the computations get easier with segment breaking.
Through concatenation, the two major theoretical results that came into existence are as follows:
- When a large number of arbitrary codes are concatenated then the probability of error shows an exponential decrease with block length. Also, there is an algebraic increase in decoding complexity.
- When there is a finite number of codes concatenated then the error exponent is less than the attained through a single stage. However, below capacity rates, it remains non-zero.
It is to be noted here that in the turbo code about which we have briefed in the introduction, the encoder units are configured parallelly and this also applied to decoder units as well.