Definition: A number system that corresponds only two numerical digits i.e., 0 and 1 is known as a binary number system. As it is a 2-digit system thus known as a base 2 system. The operation of a computer system solely relies on the binary number system. As it only understands binary values i.e., 0 and 1.
Now, the question arises why a computer system understands only binary values?
The answer to the above question is as a computer is an electronic device and all the electrical and electronic devices understand only electrical signals. So, 0 and 1 binary digits simply correspond to the off and on state of the device respectively.
The digits 0 and 1 show the same meaning as in the decimal number system. However, the variation in the position of binary numbers depends on the value being represented.
As with the increase in the position from right to left the weight shows successive increment in the power of 2.
Let us have a look at how we can write a number in binary digit in the power of 2:
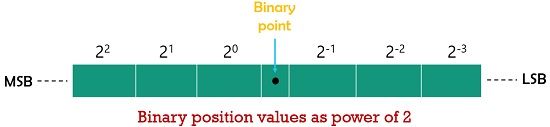
The two binary digits 0 and 1 are known as bits. A bit is considered as the primary unit of information. The word BIT is derived from a combination of BInary and digiT. However, a combination of 8 bits gives rise to another unit known as a ‘byte’. Also, when 4 bits are combined then unit ‘nibble’ is formed.
It is noteworthy here that the basic Boolean functions are based on the binary number system. One can change a binary represented value in the decimal, octal or hexadecimal system. Also, we can change any number system into binary number system by performing a proper operation.
Counting of binary numbers
As we know there exist 10 digits in decimal number system i.e., 0 to 9. However, by using the combination of these words on varying their position, multiple quantities can be represented.
Let us first understand how counting is done in binary number system then we will move further to understand its decimal representation.
Here, we have only 2 digits as the counting begins with 0 and ends with 1. However, due to the presence of only 2 digits, in successive counting, digit 1 is shifted towards left and the digit at its right becomes 0 thus providing 10 in binary which is nothing but represents 2 of the decimal number system.
The table given below will provide you with a better idea about the representation of decimal in binary and its counting format:
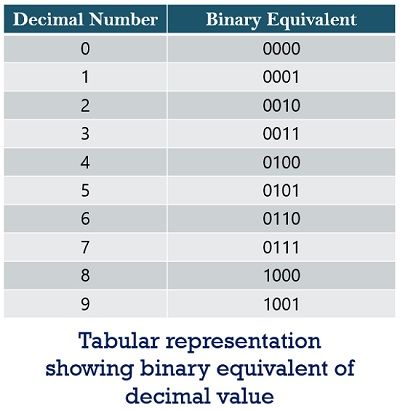
It is clear from the tabular representation shown above that a binary number exceeds in the power of 2 beginning with 0 which we have already discussed earlier.
How to represent decimal numbers in binary format
In order to get the binary equivalent of a decimal number, we consecutively perform division of the quotient term until it becomes 0. Also, we consecutively note the remainder achieved after each division. These reminders are then written in reverse order of their arrival. In this way, we simply get a binary equivalent of any decimal value.
Let us now move towards mathematical implementation of the above-discussed method:
For example, let the number be 15:
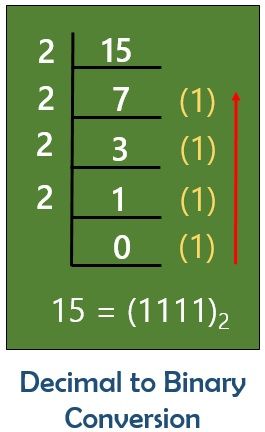
The method is known as double dabble method.
Sometimes in real life, we come across decimal numbers in fractional format. So, let us take an example of a fractional decimal number which has to be converted into a fractional binary number.
For example, let the number be 0.65:
In order to change 0.65 into a fractional binary number, the number first multiplied with 2. The resultant achieved after multiplication is further multiplied successively by 2. Also, after multiplication, the result obtained is decimal value thus the digit before the decimal serves as carrying bit.
The fractional decimal to binary conversion in the form of mathematical implementation is shown below:

Here, in this case, the carry is noted in the downward direction. It is noteworthy here that the binary multiplication is usually continued up to eight binary digits. Hence, we can say that the result obtained is not exactly equivalent but is considered as approximate value.
Characteristics of Binary Number System
- It is a 2-digit number system.
- It is commonly called a base 2 number system.
- The different positions of binary number systems show the equivalent value in power of 2.
- The leftmost position of the binary representation shows 2 raised to the power x. Here, x represents the extreme position of the left.
Advantages of Binary Number System
With the evolution of the binary number system, the operation of the various task has been simplified. By making use of binary values various logical problems that rely on Boolean algebra can be solved easily.
Uses of Binary Number System
- In electronic devices: Electronic devices like computer, diode, BJT, MOSFET etc. only operate on low and high value i.e., 0 and 1 of the binary number system.
- In punched cards: These are widely used in punched cards that shows 0 for unpunched condition and 1 for the punched condition.
- In digital computers: A digital system is based on binary values 0 and 1. The digital computers operate on binary values in order to perform logical operations.
- In magnetic tape: A magnetic tape can be utilized as a device having 2 states. As in this case some points are magnetized showing binary 1 and rest are unmagnetized representing binary 0. Thus, in this way, a reel of magnetic tape can be used to store information in binary form.
A binary number system performs various logical operations such as addition, subtraction, multiplication and division. However, among all of them, addition is most important.
I ‘m very satisfied with the explanation and I love it. 😊