Octal Number System

Definition: Octal number system is a base 8, digital number system. This number system has 8 numbers starting from 0 to 7 in its range. The numbers 0, 1, 2, 3, 4, 5, 6, 7 holds similar meaning as that in case of the decimal number system.

Oct means 8 and this is a number system with a base or radix 8. Hence it is called so.

The position of the digits in an octal number system is given as:

Now a question strikes our mind that digital circuits understand only binary values. Then,

what is the need to have octal representation?

The answer to this question is that sometimes it becomes difficult to manage the long strings of binary data or result. This leads to erroneous results.

Therefore, sometimes binary data is represented in the octal format in order to avoid the bulkiness of the information.

However, it is to be noted here that digital circuits process only on binary data i.e., in the form of 0 and 1. Thus while using the desired information in digital systems, octal to binary conversion is necessary.

The length of the octal number system is basically one-third of that of the binary number system.

Let us see an example of octal representation of a number

(745)₈ 

Here, base 8 clearly shows that it is an octal representation. It is always necessary to represent a particular number with its specific base. In case, in octal representation, base 8 is not specified, then by default, the number is considered to be decimal by the system.

Therefore, it is always important to represent a number in any number system with its desired base.

Counting of Octal Number

In the previous article of the binary number system, we have discussed the basic concept of the number system. And we know that the octal number system holds 8 digits, from 0 to 7.

The table given below represents the octal numbers. Along with that binary representation of each octal number is also represented below:

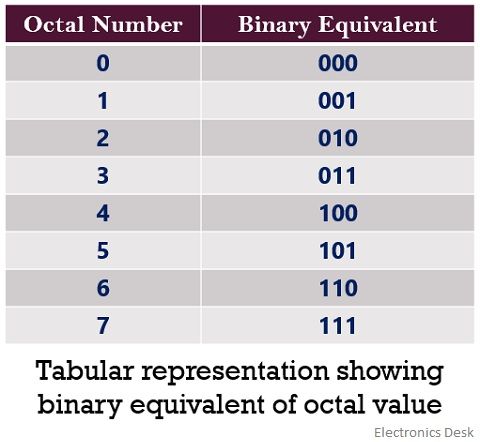
Now let us consider some examples and understand the number conversion.

Examples of Octal Number System Conversion

Conversion of Octal number to binary form

In octal to binary conversion, each octal bit is converted into its binary equivalent form. As the base of octal number i.e., 8 is the result of 2 raised to the power 3. We have already discussed the binary equivalent of octal digits from 0 to 7.

Let us take an example in order to have a better understanding of octal to decimal conversion.

(427)₈

Suppose this is the octal number that is to be converted into the binary equivalent.

By considering the table given above, we can convert each octal bit into its equivalent binary format.

Let us take another example of an octal number in fractional form:

(541.63)₈

Consider the octal number above that is to be converted into its equivalent fractional binary value.

Conversion of Binary number to Octal form

While performing the conversion from binary to octal, the reverse of the above-discussed process is performed.

Whenever a binary number is given and we have to perform its octal conversion, then the total bits of the binary equivalent is divided into the group of 3, beginning from LSB to MSB.

As we have already mentioned that the octal number system is nothing but the third power of the binary number system. Therefore is divided into groups of 3.

So, once the groups are divided, then each binary group value is assigned it’s octal equivalent value.

Sometimes in order to have a complete group of 3 bits, zeros are added to the binary values when needed.

Let see an example to understand the conversion of a binary value into octal value.

Suppose the binary value that is to be changed into octal equivalent is

(11010110)₂

Then starting from LSB, the bits must be grouped into 3 bits each

11 010 110

As we can see that the third group in the binary value is incomplete, due to the absence of the third bit. Thus, in this case, we put an additional zero to complete the third group.

Let us take an example of a fractional binary value that is to be converted into the octal equivalent.

(100111001.101010)₂

So again grouping of the bits is performed

Conversion of Octal to Decimal form

At the time of converting an octal number into decimal equivalent, each digit of the octal number is multiplied with its positional value. We have already seen the positional value chart in the introduction.

So now let us take an example to convert an octal number into the decimal equivalent.

(541.21)₈

Conversion of Decimal to Octal form

Whenever it is required to convert a decimal number into its equivalent binary value, repeated division of that number is performed to get the desired octal equivalent. But unlike in case of binary, here the division is performed with 8 despite using 2.

The method is also known as double dabble method.

Let us take an example and understand how the conversion of decimal to octal is achieved.

(478)₁₀

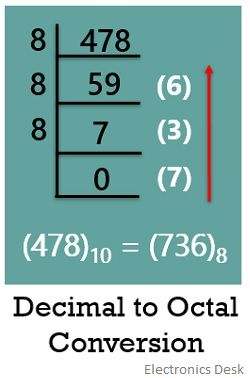
At the time of writing the equivalent octal term, we write the carry bits obtained in an upward direction.

Sometimes we come across fractional decimal values. So, the question arises how can we convert, the fractional decimal values into fractional octal value.

Consider an example, given below

(0.54)₁₀

While writing the fractional octal equivalent, the result must be written in a downward direction. Here, we have performed the multiplication up to 8 digits. Hence we get approximated value and not the exact value.

Advantages

• Size of the string in octal representation is small.
• Due to the small length of the string, chances of errors in the result are less.
• The bits can be easily converted according to the need.

Disadvantages

Every time an additional converting unit is required as digital circuits operates on only binary values. Thus, data in the octal form must be converted into binary format.