Difference Between Half Adder and Full Adder

Both half adder and full adder comes under the category of combinational logic circuits that are used for arithmetic operations. However, there exist many differences between the two. The major difference between the half adder and the full adder is that the half adder operates on 2 inputs. On the contrary, full adder operates on 3 inputs.

More specifically, we can say that half adder, adds only 2 one-bit numbers and the previously generated carry bit is not added in its case. But, the full adder adds 3 one-bit numbers, as here the previously generated carry is also taken into consideration.

Let’s have a look at the contents to be discussed under this article, further we will discuss other important differences between the half adder and full adder.

Content: Half Adder Vs Full Adder

1. Comparison Chart
2. Definition
3. Key Differences
4. Conclusion

Comparison Chart

Parameter	Half Adder	Full Adder
Operates on	2 inputs	3 inputs
Carry in from previous addition	Not acceptable due to only two inputs	Acceptable due to 3 inputs
Circuit components	Single XOR and AND gate combination	Combination of 3 AND, 2 XOR and 1 OR gate
Logic operation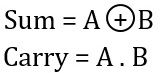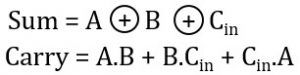
Uses	Computers and calculators etc.	For long bit addition such as in digital processors.

Definition of Half Adder

An arithmetic circuit that carries out the summation of 2 inputs of one-bit is known as a half adder.

Everyone is familiar with basic addition technique in which when two bits are required to be added then, the addition begins with the rightmost column. As there is always a possibility of carry term to exists. The same rule is utilized in the operation of half adders.

The figure below represents the logic symbol for half adder:

The figure clearly shows 2 applied inputs and 2 outputs for half adder. Out of the two, one output shows the summation while the other show carry generated.

Let us have a look at the logic circuit of half adder in order to understand its operation more clearly:

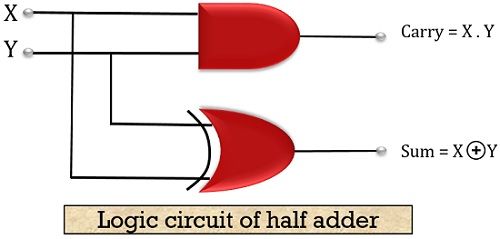
Here X and Y are the two inputs applied whereas S and C denotes the sum and carry bits. A half adder is composed of 1 AND gate and 1 XOR logic gate. The summation bit generated by the half adder is represented by the XOR operation and the carry bit generated by the half adder is represented by the AND operation.

Let us have a look at the truth table of half adder then we will summarize its operation:

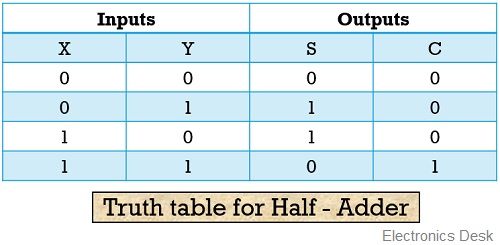Case 1: When both the applied inputs at the half adder is logic low i.e., 0 –

We know that summation of 0 and 0 will result in output 0 and in this case no any carry term is produced.

Case 2: When the first applied input is logic low i.e., 0 and second applied input is logic high i.e., 1 –

We know the addition of 0 and 1 will provide 1 as the sum but no any carry is generated in this case.

Case 3: When the first input is 1 and the second applied input is 0 –

Again the addition of 0 and 1 will generate 1 as the sum but no any carry bit will get generated.

Case 4: When both the applied inputs are logic high i.e., 1 –

The addition of 1 and 1 will generate 2 but in binary terms, we write 2 as 10. Thus, in this case, 0 will be the sum and 1 will become the carry bit.

Definition of Full Adder

Full adders are the arithmetic circuits that generate a summation of 3 inputs of one- bit.

The figure below represents the logic symbol of a full adder:

This figure clearly shows the 3 inputs applied to the full adder and the 2 outputs. Here, also the one output shows the summation result and the other shows the carry bit generated.

The figure below represents the equivalent logic circuit for full adder:

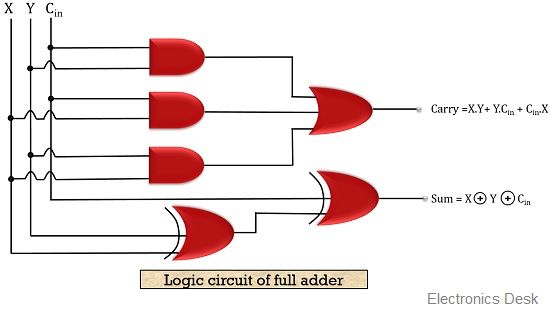Here, X, Y and C_in are the 3 inputs applied to the adder whereas S and C denotes the sum and carry generated.

Let us now analyze the truth table for full adder:

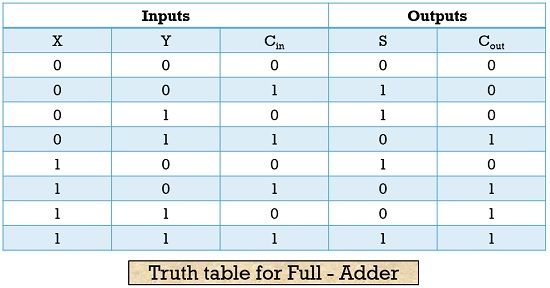
We already know the fact that if only one of the inputs is logic high i.e., 1 and the rest are 0. Then, the sum generated will be 1 and the carry will be 0.

But if out of 3, two inputs are logic high i.e., 1. Then its summation will generate 10 in binary forms representing 2. So, in this case, 0 is stored as the sum and 1 is stored as the carry. When all the 3 applied inputs are logic high i.e., 1 then, in this case, the sum generated will be 1 as well as the carry generated will also be 1.

This is so because the addition of 1 and 1 give 0 as the sum and 1 as the carry this summed output 0 is then added with the last input 1. Thereby generating 1 as overall summation and 1 as the carry.

Conclusion

So, from the above discussion, we can conclude that a half adder and full adder both performs the addition of the applied input bits. But half adder is used in a lower degree of addition operations while full adder is used for a somewhat higher degree of addition operations.