Hamming Codes are linear block codes designed to detect and correct errors introduced in message bits transmitted from an end to another through a communication channel. These are single error-correcting codes that offer ease in encoding and decoding.
Hamming Code falls under the category of error correction coding and is a type of cyclic code.
In the year 1950, R W Hamming proposed an efficient array of algorithms as a technique for error correction, which was named hamming codes. The aim behind introducing it was to detect up to 2-bit errors at the same time and can correct a single bit error.
Content: Hamming Code
- Introduction
- Basics
- Encoding with Example
- Decoding with Example
- Advantages
- Disadvantages
- Applications
Introduction
We all are aware of the fact that message signal (in the form of bits) is transmitted from one end to the other via the proper channel in digital communication. However, during transmission, a high possibility of introduction of errors within the message bits exists because of factors like noise or any other interference. Thus, detection, as well as correction of errors at the receiver, is quite an important task and this can be achieved by introducing redundancies in the actual message bits.
Error-correcting codes are used to deal with the introduction of errors while transmission. This includes error detection as well as correction.
Basically, error detection coding corresponds to the analysis where the receiver gets to know that error exists in the received sequence but fails to get the erroneous bit. While error correction coding corresponds to determining the actual bits, which is erroneous, and applying methods to correct the error bit.
Hamming codes are the ones that perform both error detection as well as error correction thereby giving rise to an efficient error correction coding system. Basically, in such error-correcting codes, redundancies are used for error detection and correction. This works in a way that, parity bits along with actual message bits are transmitted over the channel in a coded format. When the receiver gets the coded signal then it separates the parity bits from the message bit and simultaneously if the error is introduced then it gets also detected and further corrected.
Basics of Hamming Codes
In hamming codes, message bits are encoded using redundant bits. These redundant or parity bits are the extra bits that are placed at different positions within the message bits. At the receiving end, when the receiver receives the coded bits then some sort of recalculation is performed after which the error bits are obtained and necessary correction is applied.
Suppose if k denotes the length of information bits and n denotes the total length of the coded bits then the length of parity or redundant bits can be obtained by getting the difference between the length of coded bit and length of information bits i.e., (n-k).
All single error-correcting linear block codes are hamming codes and in general given as:
![]()
: 2P – 1 = n
2P – 1 – P = k
Hence,
P = n – k
Let us now proceed to understand how encoding and decoding take place.
Hamming Codes – Encoding
The steps involved to perform encoding of hamming codes are as follows:
1. First, perform the calculation for the total number of redundant bits required to be added with the given message bits. The number of redundant bits can be obtained by:
![]()
: P is the number of parity bits,
k is the number of information bits.
2. Once the number of redundant bits is detected then we have to check for the positions where the redundant bits are to be placed.
Note: The redundant bits within the message bits are placed at those positions which are powers of 2.
3. Now, determine the value of redundant bits to be inserted at the positions determined in the previous step.
The types of parity bits play a crucial role here. Meaning, if there is even parity, then the total number of 1s must be even in count. While if there is odd parity, then the total number of 1s must be odd in the count.
Let us understand how these are implemented using an example.
Example for Encoding
Suppose we are having a message signal given as:
k = 11010
and it is to be transmitted after encoding with even parity.
So, calculating the number of redundant bits using
![]()
For P =3
23 ≥ 5 + 3 + 1 = Not satisfied
For P = 4
24 ≥ 5 + 4 + 1 = Satisfied
So, we will take P = 4 for k = 5
Hence, for 5 bits of message signal, 4 bits of redundant codes will be required.
Next, we to check at which positions these 4 parity bits are to be placed. So, according to hamming, the parity bits will be present at positions which are powers of 2 i.e., 20, 21, 22, 23, 24, and so on.
So, forming the hamming code arrangement for code (9, 5). Also, placing the 4 bits of parity at the desired positions. This will be done in a way that in the 9 given blocks, according to the powers of 2, the parity bits will be present at positions,
20 = 1; 21 = 2; 22 = 4; 23 = 8
Lastly, we have to find the parity bits that are to be placed at the above-determined positions. Hence the value of parity bits from the data bits will be determined as:
P1 = D3 D5 D7 D9
![]()
This is obtained by considering the data bits in take 1 skip 1 format from the above hamming code arrangement beginning from P1 itself. Similarly,
P2 = D3 D6 D7
![]()
This is obtained by considering the data bits in take 2 skip 2 format from the above hamming code arrangement starting from P2. Furthermore,
P4 = D5 D6 D7
![]()
This is obtained by considering the data bits in take 4 skip 4 format from the above hamming code arrangement starting from p4. And after this, no significant data bits to be considered are present thus we will stop here. Similarly,
P8 = D9
![]()
This is obtained by considering the data bits in take 8 skip 8 format from the above hamming code arrangement starting from p8. But as here we do not have any data bit after D9 thus, we will stop right there in this case.
It is already mentioned in the beginning that the encoding includes an even type of parity. Thus, checking for each parity bit,
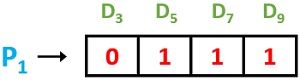
As these are odd in number thus P1 = 1 to make it even.
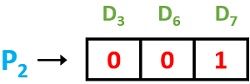
As these are odd in number thus P2 = 1 to make it even.
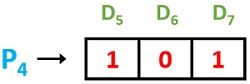
As these are even in number thus P4 = 0 to keep it even.
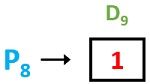
As it is odd in number thus P8 = 1 to make it even. Hence on concluding we will obtain:
P1 = 1
P2 = 1
P4 = 0
P8 = 1
So, placing the parity bits within the hamming code along with data bits we will get,

Hence the encoded sequence transmitted from the transmitter will be:
111010011
: LSB and MSB of the sequence correspond to the first and last bit respectively, as we have written in the right to left format.
Hamming Codes – Decoding
The steps involved that detect and corrects the error of the coded bits obtained are as follows:
1. Firstly, using the expression
![]()
Check for the number of parity bits present in the received coded bits.
2. Now, position the redundant bits accurately like the way we have discussed in encoding that it must be placed at positions of powers of 2.
3. Lastly, go for parity check according to even or odd parity scheme used during transmission using data and redundant bits.
Example
For detection consider that the received sequence is: 111000011
First, we have to check what is the length of message bits and parity bits individually. So, considering,
![]()
Since we know k + p corresponds to the total number of bits which is 9 here so, we can predict that k i.e., length of information bits is 5 while p i.e., the length of parity bits is 4. On checking, the condition has been satisfied thus, we analyzed that here the total message bits are 5 and total parity bits are 4.
Secondly, using the same way as we have done in encoding, the positions of data and parity bits can be obtained. Thus, in hamming code arrangement for the obtained sequence, it will be written as:

Lastly, we will go for a parity check. As the encoding is done by considering even parity. So, we will consider each parity bit and check whether it satisfies the even parity condition or not.
We have already mentioned in encoding that parity bits for hamming code are given as:
P1 = D3 D5 D7 D9
P2 = D3 D6 D7
P4 = D5 D6 D7
P8 = D9
So, from the obtained coded sequence, we will check for even parity conditions.
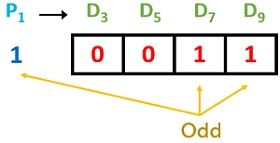
As these are odd in number thus even parity condition is not satisfied. So, whenever even parity is not satisfied then write that parity bit necessarily as 1. So, P1 = 1. Next,
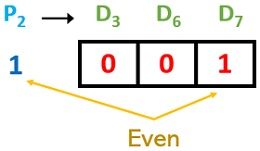
Again, even parity condition is satisfied. So, we will write the parity bit as 0. P2 = 0. Furthermore,
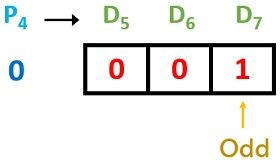
Here, even parity condition is not satisfied. So, P4 = 1. Next
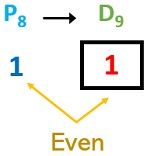
Even parity condition has been satisfied. So, P8 = 0. Therefore,
P8P4P2P1 = 0101
Now, getting decimal equivalent of the above obtained binary value.
(0101)2 = (5)10
This means 5th bit of the obtained sequence has an error.
Now, the corrected sequence will be obtained by summing the received sequence and error sequence.
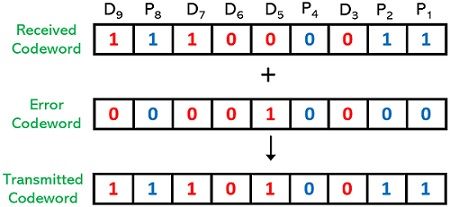
Hence, the actually transmitted (corrected) sequence will be: 111010011
Again, here the LSB and MSB represent the first and last bit respectively, as we have written in the right to left format.
Advantages
- Highly efficient for single-bit error correction.
- Easy encoding and decoding offer simplicity in error detection and correction.
Disadvantages
- It is not suitable for correcting multiple error bits.
- The requirement of transmission bandwidth is high.
Applications of Hamming Codes
Hamming codes find applications in fields such as computing, telecommunication services, like satellite communication, modems, embedded processors, etc.