The motion of satellites in space was governed by the laws of planetary motion proposed by Johannes Kepler. There are three laws, known as Kepler’s three laws that describe the motion of a satellite in space.
The first law of Kepler is also known as the law of orbits, the second law is called the law of areas and the third law is sometimes referred to as the law of periods according to the theory each specific law suggests.
Content: Kepler’s Laws
Introduction to Kepler’s Laws
Kepler’s laws are nothing but the laws that correspond to the motion of planets in the solar system. Johannes Kepler, a German astronomer, proposed three basic laws that describe the planetary motion around the sun in space. Kepler derived the three laws for describing the planetary motion after careful observations and these were not mere assumptions. However, after that Isaac Newton developed the theory of gravitation.
The laws proposed by Kepler, in general, are applied to two bodies present in space interacting due to gravitation. So, in satellite communication, Kepler’s law for motion of any two bodies is considered and the motion of a satellite around the earth in space is governed, where the heavy body is called primary while the lighter one is referred to as secondary. Thus, for the satellite orbiting earth, the primary will be the earth whereas the satellite will be secondary.
The three laws of Kepler provide idea about:
- The path of the secondary while orbiting primary,
- The area covered in space, and
- The orbital period of the secondary.
Here in this article, we will separately discuss each law but before understanding the three laws of Kepler’s for the motion of a satellite in space let us understand-
What is a Satellite?
A man-made device that rotates around the earth or any other moving object existing in space is known as a satellite. However, there exist natural satellites also like the earth which revolves around the sun, and the moon which revolves around the earth.
There are two major parts of artificial satellites which are an antenna and a source of power. The antenna is used for transmitting and receiving the signals while the power source is used to supply energy to the device for continuous operation.
Now, you must be thinking, why a device named satellite is required in space?
So, basically, various signals that require transmission from one end of the earth’s surface to the other end fail to do so as they are unable to follow the earth’s curvature or sometimes obstructed by any building, mountains or trees, etc. Thus, due to the straight-line path possessed by signals, they reach space and are captured by the satellites present there and these signals are then retransmitted to different spots on the earth surface according to the requirement. Hence in this way, the satellites orbiting earth are used.
Kepler’s First Law
According to Kepler’s first law, while orbiting the earth, the path of the satellite is elliptical in nature. An ellipse has two focal points and the earth is situated in one of two foci. This is clearly shown below:
However, you must note here that in the case of an ellipse, for a two-body system, the center of mass i.e., barycentre is situated at one of the two focal points. And as here huge difference in mass of earth and satellite exists thus the center of mass and center of the earth will be at the same point i.e., always at one focus of the ellipse.
For satellites orbiting in space, a and e are the two crucial parameters, where a is the denotation used for the semi-major axis and b is used for the semi-minor axis. And e is the eccentricity which is given as: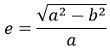
For an ellipse, e lies between 0 to 1 however the orbit becomes circular rather than elliptical when the value of e is 0.
Kepler’s Second Law
According to the second law, the satellite in the orbital plane will sweep an equal journey in an equal time interval. More simply, when the time interval is equal then the satellites in the orbital plane will cover the equal distance.
Consider the figure given below where the earth is present at the barycentre and the satellite covers distance d1 in 1 sec, sweeping out area A1 and distance d2 sweeping out area A2 in 1 sec.
The distance covered is assumed to be in meters.
So, by Kepler’s second law, A1 = A2
Here, the average velocity of the satellite to cover distance d1 and d2 is S1 m/s and S2 m/s and as areas, A1 and A2 are equal thus S2 will be less than S1.
This can be said in a way that the speed of the satellite during orbital motion is not constant thus, the satellite sweep out the same amount of areas in equal time duration. You must note here that the point where the satellite is nearest to the earth is known as perigee and the point where the satellite is farthest to the earth is the apogee. This implies that the satellite moves fast at perigee and slow at the apogee.
Kepler’s Third Law
According to the third law, the square of the periodic time of orbit shows direct proportionality with the cube of the semi-major axis, ‘a’ of their orbit. Thus, it can be written as:![]()
The third law proposed by Kepler shows that the periodic time of orbiting by the satellite shows a rapid increase with the increase in the radius of the orbit in which the satellite is moving.
This can be understood easily by considering the motion of planets around the sun where the closer planet i.e., mercury takes less time (i.e., 88 days) to orbit the sun while the comparatively distant planet i.e., the earth takes more time (i.e., 365) for the same. This is so because the orbital radius is more in the case of earth and less in the case of mercury.