Doppler effect in the radar system is a phenomenon of change in frequency of the transmitted and received signal when the object is not stationary. More specifically we can say, it defines the variation in the frequency of the signal when the object is moving in space.
This phenomenon was defined in 1842 by an Austrian physicist Christian Doppler.
Doppler Effect in Radar
We have already discussed in our previous article of the radar system, that radar is used to determine the position of an object in space by transmitting electromagnetic signal. When the signal gets interacted with the object then an echo is produced which is received by the receiving antenna of the radar system.
And in case of moving object, the frequency of the signal received is different from the one that is actually transmitted. And this frequency shift is an outcome of the movement of the target.
Here in this article, we will discuss the variation in the frequency with respect to the movement of the target.
So, the basic point that is needed to figure out here is how the variation in frequency is interpreted in case of an object in motion?
Basically, there exist two cases that show the change in frequency according to the Doppler effect.
- When the target approaches or moves closer to the radar then the wavelength decreases. Thereby increasing the frequency of the signal.
- While in case the target moves away from the radar then increase in wavelength is noticed and so there exist a decrease in frequency.
Basically, for a moving target, the speed of movement is also needed to be determined by the radar system. So, the Doppler frequency shift i.e., the difference of originally transmitted frequency to the received frequency shows the speed of the object.
It is to be noteworthy that here we are discussing the Doppler effect of radar system but it is applicable for all wave motion.
Let us first understand in detail about the variation in the frequency with respect to the movement of the target.
We know in case of a stationary object, the frequency of the signal/sound produced by the radar is equivalent to the frequency of the signal/sound received by the radar after interaction with the target in space.
The reason behind this is that due to a stationary position, the waves transmitted every second by the radar will be equivalent to the number of waves received.
But if the target is non-stationary and is moving towards the radar then, in this case, a large number of sound waves will be received by the radar per second after being interacted by the target. And so greater number of waves indicates the increase in frequency.
Thus doppler shift will be high in this case.
As against when the target is moving away from the transmitter then the number of waves received per second gets reduced. Thereby indicating a reduction in frequency.
But the frequency of the signal from the transmitter is constant for both the cases. Still, the movement of the target is variating the frequency of the received signal.
Derivation of Doppler Frequency
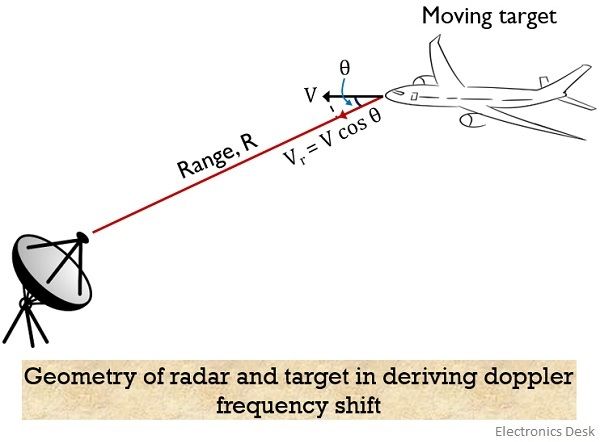
Suppose a continuous wave is emitted by the transmitting antenna of the radar system and the target is present at a distance R from the radar. Also, consider the relative speed of the target with respect to radar is Vr along the line-of-sight. And the frequency of the emitted continuous wave is f0.
Let n be the total number of wavelengths in the path between radar and target in both the direction and it is given by:
It is to be noted that an angular excursion of 2π is corresponding to a single wavelength.
Therefore, the total angular excursion is given by:
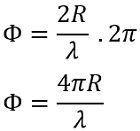
With the movement of the target, R and φ both show variation.
Thus we can say the change in φ wrt time is the angular frequency. Also known as Doppler angular frequency.
And is given by
So, further on simplifying we get,
Since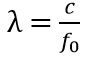
Therefore,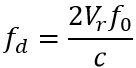
This is the equation for the doppler frequency.
The relative velocity in case of moving target is given as:
: V is the velocity of the target and
Θ denotes the angular target velocity vector.
For θ = 0⁰, maximum Doppler frequency is achieved.
While for θ = 90⁰, the doppler frequency is minimum i.e., 0.
It is to be noted here that the shift in frequency is positive for a target moving towards the radar. Whereas negative for the movement of the target away from the radar.