In the previous lecture, we have discussed the basics of radar and how radar is used for detection and location of an object in space. But the question arises is there any limit which specifies the range up to which this detection is possible?
So the answer to this question is yes, there exist some factors that decide the range of the radar. And these factors combinely form the radar range equation.
The radar range equation is used to evaluate the particular range up to which the object or target detection is possible.
The equation is related to various factors of the radar system like characteristics of transmitting, receiving antenna, object/ target and the effects of the environment on the transmitted signal. While designing a radar system, the radar range equation is an important aspect because it shows the range up to which the system can detect the target.
In this section, we will derive the range equation for a radar system. So, let us proceed further and understand how the range of a radar is detected.
Derivation of Radar Range Equation
Consider
- R denotes the distance of the object from the transmitting antenna,
- σ denotes the cross-sectional area of the object,
- Pt denotes the maximum amplitude of transmitted power,
- Pr is the maximum amplitude of power received by receiving antenna,
- Gt is the power gain of transmitting antenna relative to an isotropic radiator,
- Gr is the power gain of receiving antenna,
- Ae is the effective area of receiving antenna,
- Smin denotes the minimum amplitude of the signal that can be detected by the antenna at the receiving end.
Consider that the transmitting antenna is isotropic in nature thus it radiates the transmitted power in a uniform manner in all the directions.
Then the power per unit area i.e., power density will be given as: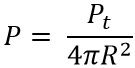
It is the ratio of transmitted power by the antenna to the surface area of the imaginary sphere i.e., 4πR2. Here R denotes the radius of the sphere.
Its unit is watts/m2.
Usually, radar systems use a directive antenna with narrow beamwidths that direct the radiated power in a single direction.
The antenna gain specifies the power density in the direction of the directive antenna to the power density in that particular direction by an isotropic antenna.
Thus is written as
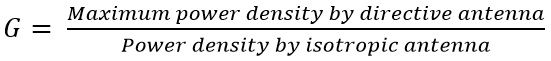
Therefore, the power density by the directive antenna at the object is given by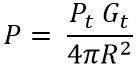
We know the signal transmitted by the radar when intercepted by an object in space then the energy gets re-radiated in different directions.
And this leads to the reception of a part of transmitted signal i.e., echo by the receiving antenna.
However, the reflecting ability of the object is specified by its cross-sectional area.
Suppose P is the power incidenting on the object and is given by: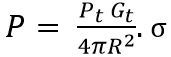
So, the reflected power density at the radar system is given by:
The antenna at the receiving section of the system captures a part of the echo signal reflected by the object/ target.
However, the power received by this antenna will be the product of power incidenting on the receiving antenna and the effective area of the antenna.
This is given by:![]()
: Ae is given by A.ρa
Here A is the physical area and ρa is the antenna aperture efficiency.
Therefore,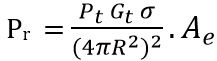
More simply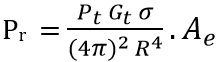
The distance beyond which the object cannot be identified is defined as the highest range supported by the radar. And this happens when received echo becomes equal to the minimum detectable signal Smin.
So substituting Pr = Smin and transposing R to the LHS we get the maximum supportable range of the radar system. And it is given by:
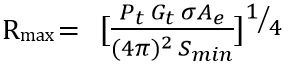
This equation is known as the radar range equation.