Input Impedance of Antenna

Definition: The input impedance of antenna is basically the impedance offered by the antenna at its terminals. It is defined as the ratio of voltage to the current across the two input terminals of the antenna. Generally, the antenna impedance is given as:

We have already discussed in our previous article that antennas are used in wireless communication in order to transmit the signal in the form of waves. It is designed to change electrical energy into the electromagnetic signals at the transmitting end. While electromagnetic signal back to electrical one at the receiving end.

So, it basically integrates the electric field and magnetic field in order to generate voltage and current so as to actuate electrical devices. Thus the antenna impedance at a point is also given as the ratio of electric field to the magnetic field at that particular point.

Hence we can say that the impedance provided by the antenna at its input terminal is known as antenna impedance.

We know that when a certain voltage is provided to any transmitting antenna then it generates current by following ohm’s law.

Here R represents the resistance of the input terminal of the antenna.

Further on considering the imaginary part, we will have

So, if we have a transmitting antenna that is radiating some power then impedance Z will be present behind it. This is known as the impedance of the antenna.

This impedance is a merger of resistance and reactance thereby forming a complex value.

Antenna Resistance

Suppose we have an antenna with input terminals x and y:

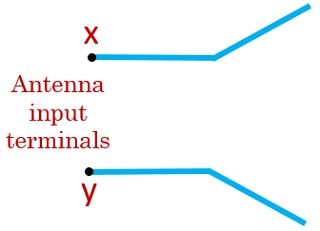
The power radiated by the input terminal of the antenna is given as: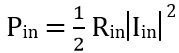

Since the total input power is the sum of radiated power and power loss,

Thus we can write it as:

This is so because all the supplied power is not radiated as some amount of power is lost.

Hence the radiated power will be: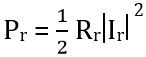

While loss / dissipated power will be: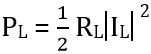

On substituting the obtained value of P_r and P_L in eq 1, we will have: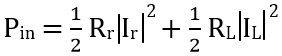

Also putting the value of P_in we will have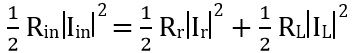

As the total current will be the sum of radiation current and loss current. Therefore writing the above equation as:

On simplifying

Thus we can say that the input resistance will be the sum of radiation resistance and the loss resistance. Therefore the figure below represents the input impedance of antenna:

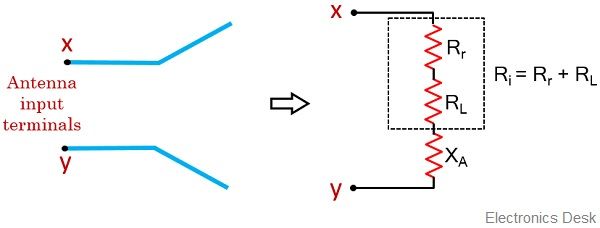
Derivation of supplied power to the Antenna

Suppose we have a configuration given below:

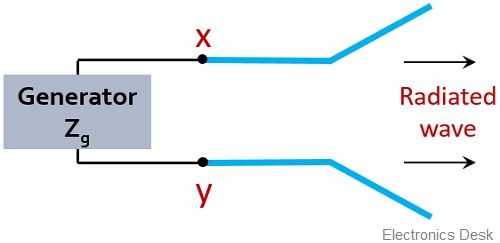
Here the two input terminals x and y of the antenna are connected across a generator.

One must note here that the generator will also have some internal impedance. So, consider the impedance of the generator be Z_g.

We know that the impedance is given as:

Therefore

• Here R_g denotes the resistance of the generator
• While X_g denotes reactance of the generator

So, drawing the equivalent circuit of the generator antenna configuration given above:

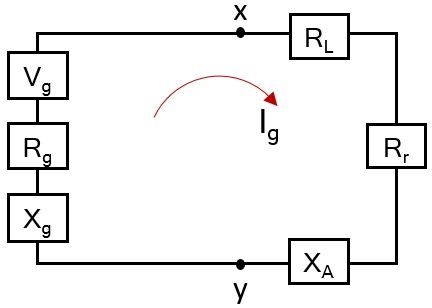
For transmitting antenna, the impedance will be given as

• Here Z_A is the impedance of the antenna,
• R_A is the antenna resistance,
• X_A denotes antenna reactance

The resistive part of the antenna which we have already derived is given as:

Let us now consider the Thevenin’s equivalent circuit shown above in order to determine the power delivered to R_r for radiation and the power dissipated in the form of heat in R_L.

So, firstly we need to determine the current within the loop itself,

Therefore, by ohm’s law

Here V_g is the maximum generator voltage while Z_t denotes the total impedance present in the loop. Thus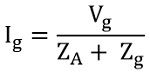

Further on simplifying,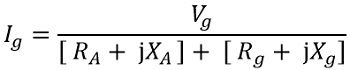

Since R_A = R_r + R_L

Therefore, we will have

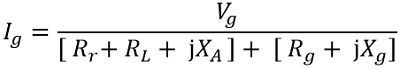
Further

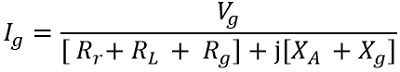
So, considering the magnitude form

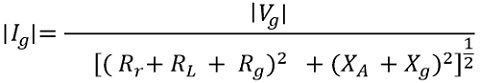
Thus we can say the radiation power P_r will be

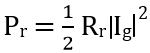
So, on substituting the value of I_g

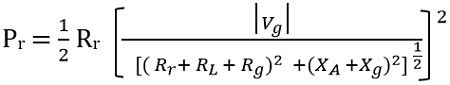
Thus the power by the generator to the antenna for radiation will be

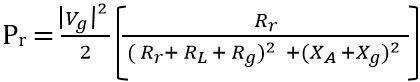
The dissipated power

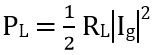
Therefore

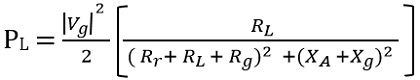
Also, the power dissipated on the internal resistance of the generator will be given as:

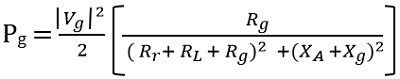
 The condition of maximum delivered power to the antenna is achievable in case of conjugate matching. This means

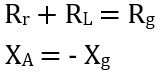
So, we will have

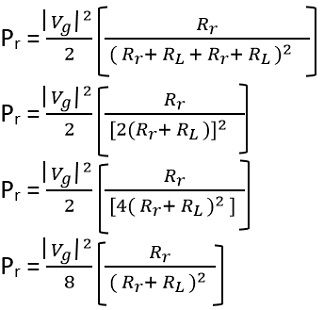Similarly

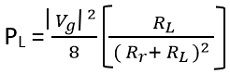
And

It is noteworthy here that the generated power must be equal to the sum of radiated power and the dissipated power in the form of heat.

So, on substituting

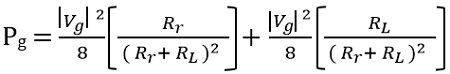
The supplied power by the generator

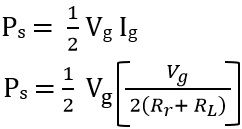
Therefore,

So, we can say the overall power generated by the generator is the sum of the power dissipated by the internal resistance of the generator and the power supplied to the antenna, in case of conjugate matching.

While, out of the overall power which is supplied to the antenna by the generator, a part is radiated utilizing radiation resistance, while the rest is dissipated in the form of heat. This dissipated power in the form of heat alters the efficiency of the antenna.