Definition: Fading in wireless communication is defined as the fluctuation in the strength of the signal received at the receiver. These are basically unwanted variations introduced at the time when the signal propagates from an end to another by taking multiple paths.
Fading is said to be a common characteristic of sky wave signals that propagates utilizing wireless communication.
Introduction of Fading
We are aware of the fact that wireless communication supports multipath propagation. This multipath propagation is nothing other than the outcome of several atmospheric reflections. So when waves of a signal from an antenna transmitted at the same time then multipath propagation causes the reception of waves in different time spans at the receiver.
The waves when propagate through different paths suffers variation in height and ionization density in the ionospheric region of the atmosphere. We are also aware of the fact that the actually received signal is the vector sum of the waves received at that instant at the receiver.
These received signals from different paths at the receiver either get added constructively or destructively.
This causes the variation in the overall strength of the received signal. Thus is known as fading.
It is noteworthy that due to fading the strength of the signal shows variation from a few dBs to around 10 or 20 dB. This depends on the condition that whether fading is normal or severe.
Fading is a gradual phenomenon and signal can be recovered. However, the fade-out is a phenomenon which is a condition of sudden ionospheric disturbance or ionospheric storms in sunspot cycles, etc. that leads to complete fading of the signal.
We have already discussed that sudden ionospheric disturbances i.e., SID is an unpredictable event. Thus fade-outs are said to be quick events that occur in the atmosphere.
Types of Fading
The various types of fadings experienced while radio wave propagation are as follows:
Selective fading
It is also known as frequency selective fading. Basically when waves propagate through different paths by being reflected from various man-made entities then the different frequencies get affected to different degrees.
This will lead to cause variation in the amplitude and phase of the signals to a different extent while propagating in the channel.
It is to be noted that even if the path length through which the signal is propagating is same, then also the signals will possess different wavelengths. This causes variation in the phase of the signal across the overall bandwidth.
Selective fading can occur over a quite large range of frequencies. Suppose signals are utilizing ground wave propagation and sky wave propagation, then in such case the phase of the signals will change with time as the two are using two different medium of propagation.
Thus combinely when the signals are received at the receiving antenna then there will be changes in the received signal from the actually transmitted one.
So, as this type of fading is frequency selective, thus at the time of propagation, even adjacent parts of the signal fade independently even if their frequency of separation is small.
Hence we can say, this causes severe distortion of the modulated signal.
As it severely affects high-frequency signals thus is more dangerous in case of sky wave propagation. The amplitude modulated signals are generally more prone to such distortions rather than SSB signals.
Thus one can use SSB systems to reduce selective fading.
Interference fading
Interference fading is also a result of the multipath propagation of signals transmitted from the antenna. It occurs when waves interfere at the channel while propagating from an end to another.
Suppose a signal is propagated through sky wave propagation, then the waves travel by getting reflected from the upper and lower regions of the ionosphere. Sometimes the waves propagate through single or multiple hops also, in case of low-frequency signals. Thereby leading to cause interference of signals in the channel.
The figure below represents interference fading caused due to the propagation of rays through multiple paths:
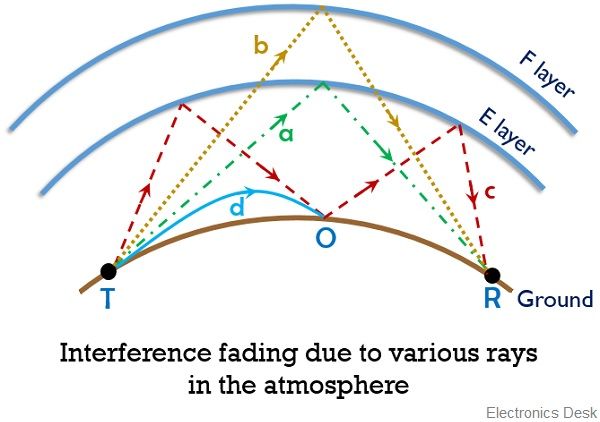
- Here ray ‘a’ is reflected from E layer,
- ray ‘b’ is reflected from F layer,
- ray ‘c’ is multihop propagation and
- ray ‘d’ is groundwave.
It is noteworthy here that sometimes it occurs even due to variation in the ionization density. Basically with the variation in path length, there is random variation in the phase and thus amplitude changes continually thus cause interference of waves.
Absorption fading
We know that when the signal propagates from an end to another then there are losses that are introduced by the transmission medium. Generally, when the signal is propagated through any medium, then the medium possesses some amount of signal absorption.
However, the amount of signal being absorbed by the medium is not constant as this depends on various factors. Thus it will be wrong to say that every transmitted signal suffers an equal amount of absorption while propagating through the same medium.
So, due to the absorption of the signal by the transmission medium, the strength of the signal varies and this deteriorates the received signal.
Polarization fading
Polarization fading is the result of variation in the polarization of the waves reaching the surface of the earth.
In sky wave propagation when wave reflects back to the surface of earth then its polarization changes. The change in polarization of the reflected wave is the result of the superposition of other waves (ordinary and extraordinary) with opposite polarization that are having different amplitudes and phases.
This leads to cause change in polarization of the wave continually with the antenna. Hence the amplitude of the signal received at the receiver also varies.
Thus is known as polarization fading.
Skip fading
Here the name itself is indicating that this type of fading is associated with skip distance of radio wave propagation.
It generally occurs near the skip distance region. This type of fading is an outcome of variation in the height and ionization density of the ionospheric region.
We are aware of the fact that skip distance is the region between transmitting and receiving point where the signal is received after getting reflected from the ionosphere.
So, the variation in the ionization density will undoubtedly alter the skip zone. This variation can be a point either in or out of the skip zone.
Now the question arises on how to deal with fading?
So, generally, a method commonly used to reduce fading is to use automatic voltage control at the receiving section. But this does not act as a complete solution because it does not show usefulness when the signal level reduces below the noise level.
As in such a case, the amplification will not be of any use. Also, this method does not support selective fading. Thus a diversity reception system is used to reduce the fading of the signal.